In two words: by asking scientific questions that lead to that!… but by having a higher awareness of the philosophical issues related to science than the average chemist.
Roughly speaking, it is at the end of my chemistry PhD (defended in December 2006) that epistemological questions about the ‘basic equation’ of chemical kinetics led me to study the history and philosophy of science quite seriously. This ‘basic equation’ is of course the rate law, which governs the rates of chemical reactions (translation note: in the francophony, this law is called van ‘t Hoff law, the same name as the law governing the equilibrium constant! But apparently, in English-spoken countries, it holds only for the second case). Why these questions?… Simply because the results of my doctoral works led me to this! Some explanations are required here.
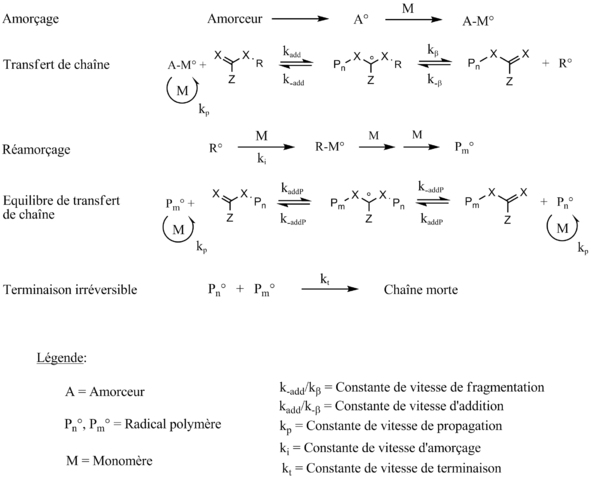
I used a polymerization process, called RAFT polymerization, extensively during my PhD work. The RAFT process is a special type of radical chain polymerization: without an additional component that is added to perform RAFT polymerization, it is a ‘conventional’ polymerization. The synthesis of this type of additional component – which is called a ‘chain transfer agent’ – was a significant part of my PhD works. But it turns out that no one really understands why the polymerization rate is (mostly) slower during a RAFT polymerization compared to a conventional one: if we apply the rate law to the known mechanism of a RAFT polymerization, we end up with the same equation as during a conventional polymerization: basically, as chemical equilibriums are set up, there are many terms that are simplified and we end up with the ‘classical’ equation.
Personally I found it a bit strange not to find any record of the complex mechanism of RAFT in the final result, because it was against my ‘intuitive’ understanding of the process; But as one should of course be suspicious (very often) of the primary intuition in science, I did not initially consider this minor annoyance. In short, in theory it is supposed to go as fast as a conventional polymerization, but in practice we can see that a RAFT polymerization is (often) much slower! This is called a ‘retardation phenomenon’. Between 2000 and 2006, two research teams were fighting for resolving this phenomenon, each giving their possible explanation by modifying the reaction mechanism (or by constraining some of the rate constants): two relatively different hypotheses were then in place.
But by repeatedly encountering experimental results that did not support either one of the hypotheses or the other, a weak consensus was reached in the polymer science community since 2006: it was probably necessary to consider the conjunction of both hypotheses at the same time in order to understand the retardation phenomenon.
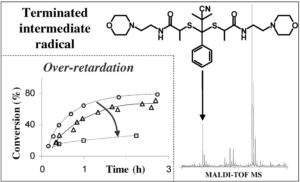
However, on my side, without being initially interested in the kinetics of RAFT polymerization, I was confronted during my PhD work (at the end of 2005) with even slower RAFT polymerization rates (in comparison with a so-called ‘classical’ RAFT… therefore already slower than a conventional polymerization)! It is by trying to understand this ‘over-retardation’ phenomenon that I entered the debate by presenting a poster in an international conference (poster on the top right of this page) and then by publishing the corresponding article in a scientific journal. What is not explicitly stated in these two publications is the fact that these results challenge, according to me, the weak consensus of the moment (but it is written quite clearly in my thesis manuscript on pages 158 and 159). In short, according to me, we don’t even have the beginning of an explanation for the retardation phenomenon!
As I have confidence in the competence of my peers in the discipline, but as they have been trying for 6 years to modify (on somewhat in all directions) the mechanism of RAFT polymerization without obtaining any convincing result in the end, I considered that I should explore another direction. And here I was wondering, which I didn’t know yet to be, in a certain sense, a heretic question (with respect to what I would learn to be the paradigm of polymer science): is the rate law really suitable to describe the RAFT process? … and to continue logically on the following question: but by the way, where does this law come from? These are probably the first epistemological questions that I really seriously considered in my research activity … even before I knew what epistemology was and that this particular scientific field existed!

After a few brief searches on the internet, here I am at the library of the University Lyon 1 looking for a copy of “Etudes de dynamique chimique” by Jacobus Henricus van ‘t Hoff published in 1884. In short, it is a very old law and it appears that J.H. van ‘t Hoff received the first Nobel Prize in Chemistry in 1901 for (among other things) this work. Nevertheless, both this ancientness and this award do not prevent the totally empirical character of van ‘t Hoff’s kinetic law. The basic principle of an empirical law is that it works as long as it works… but the time when it does not seem to accurately describe an atypical phenomenon, it is then legitimate to wonder if we have not gone beyond the field of validity of this law (and therefore it is also legitimate to try to find another one more appropriate to this `resistant’ phenomenon). The small problem is that one never learns during the training of a chemist either the empirical character of van ‘t Hoff’s law, or the epistemological limits of an empirical equation. Personally, a little interest of mine for philosophy since the final year of high school made that I was a bit familiar with some notions of philosophy of sciences (by some self-educated readings, but also having attended a small module of history and philosophy of sciences proposed by my doctoral school). For the funny story, the sentence highlighted at the bottom of the page of this web site was already in epigraph of my thesis manuscript.
Furthermore, I had been surprised in the original works of J.H. van ‘t Hoff by the absence of definition of the proportionality constants in the presentation of his law (the famous ‘velocity constants’, usually noted kx). This is not necessarily surprising for an empirical equation, but it revealed the author’s lack of interest in giving a real chemical/physical meaning to these kx rate constants: they were just proportionality constants linking the reaction rate to the concentrations of reactants, and that’s all. I must admit that I was somewhat disappointed by this finding.

Dear Henri, why are you annoying polymerists here?!
I then tried to give some physical meaning to these rate constants in the specific case of radical polymerization. Combining this research with a very personal and ‘intuitive’ understanding of the RAFT polymerization mechanism, I then proposed a new chemical kinetics equation for chain reactions: it turns out that van ‘t Hoff’s law becomes a perfect approximation of this new equation in the case of a conventional polymerization, but in the case of a RAFT polymerization there are additional terms that are not negligible. I then compare this equation to the experimental kinetic data of the literature… and it works really well ! Very confident, as I am in the period of writing my thesis manuscript, I write an appendix of about twenty pages where I try (rather awkwardly I must admit with the retrospect of years) to explain my approach and the use of the new kinetic law to better understand the RAFT process. In this appendix, I perform (without knowing it at the time) what should not be done if one wants to stay in the paradigm of the polymerists (in the sense given by Thomas Kuhn): I quote the initial work of J.H. van’t Hoff (whereas one usually limits oneself to a maximum of 10-15 years of age in the bibliography), I make a reminder about the strict mathematical definition of what is the integration of a mathematical equation (and most polymerists are not really ‘math geeks’), and I even evoke Zeno’s Paradoxes by quoting a philosopher, Henri Bergson. And so here it gets tricky!
First of all, I must emphasize the humility of my PhD supervisors, who felt overwhelmed by my somewhat complicated thinking on chemical kinetics equations, and considered themselves incompetent to judge the scientific quality of the content of this appendix. This was quite normal for polymerists specialized in the synthesis of complex macromolecular architectures, but not particularly interested in the problems of chemical kinetics. But then, they deferred this task to the referees of my PhD committee by choosing experts (of course from the same field, because the quality of the 280 other pages of the manuscript had to be evaluated as well) having a little more interest in the problem of kinetics of RAFT polymerization. So I send my PhD manuscript containing this appendix to the referees. And there, it is the drama!
I’ll give you the short story here, avoiding the epistemological aberrations that I heard: it simply ended at the jury’s deliberation during my PhD defense with my obligation to withdraw the appendix, highly problematic in their opinion, in the final version of my PhD manuscript (which, apart from the appendix, had nevertheless been considered as an excellent work)! The only sign of the initial presence of this appendix that remains in this final version is the identical last sentence on pages 159 and 222 (initially followed by a reference to the appendix).
In short, without knowing it, I was presenting a modest work of critical epistemology (concerning the sub-discipline of ‘chemical kinetics’) to polymerist researchers, who were obviously very skilled in their field of expertise, but who had never been trained (neither from afar nor closely) in epistemology: so inevitably, it could only end in mutual misunderstanding. ☹ Of course, I didn’t convince anyone of the plausibility of my results, but it was the same the other way around: no one was able to show me how my inquiry process was not legitimate and/or was flawed. So, I didn’t give up…
Since the new equation I was proposing was finally as empirical as van ‘t Hoff’s law, it was an idea to try to find a physical justification for it that was much more robust than my few intuitions and epistemological considerations that I had presented in the withdrawn appendix. Of course, I checked beforehand that there was no physical justification for van ‘t Hoff’s law, but the bibliographical research I was doing at the time only brought me to works concerning the physical justification of another important law of chemical kinetics, Arrhenius’ law (I must admit, however, that this is a bibliographical search that I should perhaps pursue again in order to confirm this absence of works concerning van ‘t Hoff’s law).
As the driving force of all chemical reactions is the thermal agitation of molecules, I began a small historical and epistemological investigation of our knowledge of this phenomenon. It turns out that the phenomenon of thermal agitation is intimately connected to the final acceptance of the atomic idea at the very beginning of the 20th century (notably the work of Jean Perrin in 1908). And here I am, very quickly, diverging towards the history of the contemporary atomic model and that of the early development of quantum theory (notably the pioneering works of Planck and Einstein). In short, I moved from chemistry to the history and epistemology of physics.
At the same time, I notice that the existence of the phenomenon of thermal agitation, which seems to indicate that there is no immobility at the microscopic scale, contradicts the conclusion that Zeno of Elea would like to reach by proposing these famous ” Motion Paradoxes ” (i.e. that motion would only be an illusion). In short, I started to be very interested in these “Paradoxes”, and therefore incidentally also in the notions of rest vs. motion. By accident, these two notions are fundamental in other works of a scientist already mentioned above; so even if I read Einstein for his contribution to the quantum theory, here I am also reading him for his elaboration of the special relativity theory. Of course, this also implies to be interested in the principle of relativity stated by Galileo. In brief, I’m still in full physics with all this!
And this is how I went from a problem of polymerization kinetics that appeared at the very beginning of the 21th century to the history (at the end of the 19th and the beginning of the 20th century) of the two pillars of modern fundamental physics. As I hope to do a serious job, I first focused on the oldest philosophical problem whose resolution (or rather non-resolution in this case!) determines, it seems to me, the framework of thought in which all physical theories were then built: how to conceptualize the passage from immobility to motion? This problem is at the very heart of Zeno’s famous ” Motion Paradoxes “. So I started with it, but my work on this subject is really not an end in itself… it is only the beginning of the challenge…
Source (before modification) of the article’s illustration image: http://wise.ssl.berkeley.edu/gallery_thesky.html
Other sources of the illustration images: https://commons.wikimedia.org/wiki/File:Vant_Hoff.jpg ; https://commons.wikimedia.org/wiki/File:Henri_Bergson_(Nobel).jpg